Entrar
Últimos assuntos
» Colisões não funcionandopor RastaMaan Sex 26 Abr 2024, 19:49
» Como ajustar velocidade de cada frame da animação no game maker
por pequetux Sex 26 Abr 2024, 16:45
» Preciso de ajuda
por AftonDuGrau Dom 21 Abr 2024, 20:18
» Como faz o evento drawn GUI, não se repetir?
por aminaro Sex 19 Abr 2024, 20:30
» PROBLEMAS COM FÍSICAS DE ÁGUA
por aminaro Ter 16 Abr 2024, 10:07
» Retorno da GMBR!!!
por Ralphed Sex 12 Abr 2024, 22:45
» JOGADOR PARANDO NO AR QUANDO ATACA
por aminaro Qua 10 Abr 2024, 13:51
» Problemas com texto interativo
por Kaaru72 Dom 07 Abr 2024, 11:31
» Erro escondido e indecifrável
por dev_gabize.azv Qui 04 Abr 2024, 10:11
» Mudar cor de apenas uma palavra
por Ralphed Sáb 30 Mar 2024, 00:39
» Procuro Programador de game maker
por Wou Sex 15 Mar 2024, 10:27
» Mod APK
por gamerainha Qua 13 Mar 2024, 06:30
» Aceito pedidos de sprites (Com exemplos meus)
por Sevilha Qua 28 Fev 2024, 12:17
» Inventário simples
por Isquilo_Roedor Qui 22 Fev 2024, 15:18
» Problemas na programaçnao de inimigo [jogo DOOM LIKE]
por Black Mirror Dom 11 Fev 2024, 13:34
» ANDROID MULTI TOUCH
por DiegoBr Dom 04 Fev 2024, 12:13
» Servidor de Discord do fórum?
por Lighter Sáb 27 Jan 2024, 17:18
» Save e Load Json
por Klinton Rodrigues Qui 25 Jan 2024, 11:12
» Colisão com mais de um objeto
por aminaro Seg 22 Jan 2024, 15:02
» Oi sou novo aqui
por Thiago Silveira Alexandre Sáb 20 Jan 2024, 20:55
» Como acessar conteudo comprado no marketplace
por macmilam Sex 19 Jan 2024, 07:42
» Devlogs em vídeos do Block Room
por Joton Seg 15 Jan 2024, 16:56
» Alguém aqui já ganha dinheiro com seus games?
por Joton Seg 15 Jan 2024, 16:49
» ACERVO GMBR MAGAZINE
por Joton Qui 11 Jan 2024, 19:21
» como aumentar o obj sem aumentar a colisão??
por GabrielXavier Qua 10 Jan 2024, 07:21
Inclinações e alguma trigonometria
GMBR :: Ensine & Aprenda :: Tutoriais :: Game Maker
Página 1 de 1
 Inclinações e alguma trigonometria
Inclinações e alguma trigonometria
Saudações, pessoal!
Decidi vir com este tutorial por um motivo bem simples: sempre notei que alguns usuários sentem alguma dificuldade com as relações trigonométricas e o Game Maker.
"Mas quando", alguém pergunta, "posso precisar utilizar trigonometria no GM?".
R: Em qualquer jogo 3D. Em qualquer momento em que haja mira angular. Em qualquer momento que precise "lapidar" os movimentos. Enfim, dominar essa técnica será muito útil.
Isto é um tutorial, então devo ensinar a fazer algo. Como quero passar um pouco do que sei a respeito de trigonometria, faremos algo bem icônico: descobriremos a inclinação de uma reta tangente. Calma, não será uma aula de Derivada. Sabe a reta tangente, aquela que só toca em um ponto da figura? (Há definições mais abrangentes, mas essa servirá). É ela que você usa quando calcula a velocidade média (espaço sobre o tempo). E se souber como utilizá-la bem, poderá corrigir vários bugs irritantes facilmente.
Para começar, ligue os motores de um novo projeto (estou usando aqui o GM 8.0 PRO, você pode me chamar de atrasado se quiser) e crie um objeto.
Para isto, só utilizaremos dois eventos.
No evento Create, declare as seguintes variáveis:
Nem precisava de tudo isso, mas quero deixar as coisas mais claras possíveis. Basicamente, estamos dizendo que o objeto estará no centro da Room, o ângulo inicial será de 360 (ou 0, se você insiste). Das outras variáveis falaremos no próximo evento que será... agora.
DRAW
É aqui que a mágica acontece.
Em primeiro lugar, vamos estabelecer o tamanho do círculo. (Trigonometria, lembra?) Você pode evitar isso e voltar no Create, colocando o valor que quiser em r. Mas eu acho mais didático adicionar isso no Draw:
Só mais um detalhe:
Agora vem a parte legal.
Não desista ainda. Vamos com calma. Em Matemática, o cosseno refere-se ao eixo x, a ordenada horizontal, enquanto o seno colabora com o y. O GM não entende bem os ângulos como aprendemos no colégio. Ele usa radianos. 180º = π , em radianos, por exemplo. Por isso usamos a função "degtorad", ela converte graus em radianos.
Agora o que viria a ser esse "diferencial+angle" e o oposto? Bem, em Matemática, há um conceito bem útil chamado Limite. Basicamente, ele diz que um valor pode se aproximar muito de outro, sem realmente chegar nesse último, com valores infinitamente próximos daquele, mas nunca exatamente. O GM tem um probleminha com isso. Se você começar a dividir muito um número, ele não se aproxima de zero, depois da quarta casa decimal ele realmente chega a zero. Por isso, precisamos de um artifício: dois pontos, um muito próximo do outro. Próximo quanto? Volte no Create. 0,001 é próximo o bastante?
Assim: ptx1 e pty1 são as coordenadas do primeiro ponto e ptx2 junto à pty2 são as coordenadas do segundo ponto. Eles estão muito, muito próximos, mas não no mesmo lugar. Portanto, se você traçar uma linha que passe nesses dois pontos, parabéns, terá traçado a reta tangente.
Isto aqui só vai dar uma ambientada na Room para ela parecer um plano cartesiano:
Agora vamos desenhar os dois amiguinhos que estão muito perto, mas não exatamente no mesmo lugar:
Agora, mais uns cálculos e eu juro que terminamos:
Note que esses cálculos para xx e yy são muito parecidos com os para ptx e pty. Qual a diferença? Simples: eles não tem o diferencial, ao mesmo tempo que levam em conta a sua existência lá atrás. Representam o ponto médio, onde a nossa reta deve obrigatoriamente passar. Ela sai desse ponto médio rumo ao longe passando por dir1 que é o nosso primeiro ponto, e para o outro lado, passando por dir2, que é o segundo.
E agora, o grande final, onde você desenha a dita cuja, a reta tangente:
Pessoal, essa foi uma demonstração de como utilizar certos artifícios no GM. Isso significa que você pode decompor fragmentos para usar no cotidiano. Afinal, a não ser que seja professor de matemática também, pode não precisar de um demonstrativo de seno, cosseno e tangente todos os dias.
Aqui você pode baixar a engine
(https://www.mediafire.com/?3b6vwoklpu6taue)
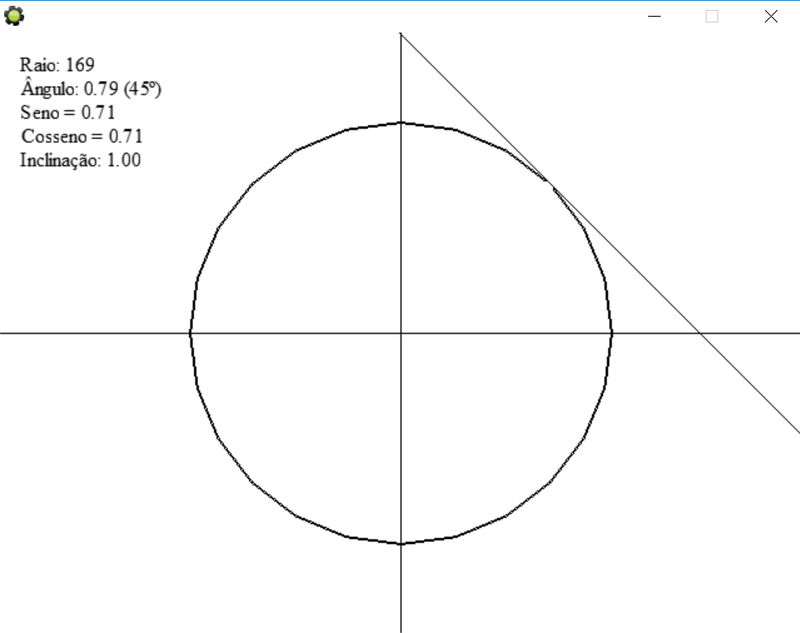
O resultado desse pequeno aplicativo que criamos é este:
Decidi vir com este tutorial por um motivo bem simples: sempre notei que alguns usuários sentem alguma dificuldade com as relações trigonométricas e o Game Maker.
"Mas quando", alguém pergunta, "posso precisar utilizar trigonometria no GM?".
R: Em qualquer jogo 3D. Em qualquer momento em que haja mira angular. Em qualquer momento que precise "lapidar" os movimentos. Enfim, dominar essa técnica será muito útil.
Isto é um tutorial, então devo ensinar a fazer algo. Como quero passar um pouco do que sei a respeito de trigonometria, faremos algo bem icônico: descobriremos a inclinação de uma reta tangente. Calma, não será uma aula de Derivada. Sabe a reta tangente, aquela que só toca em um ponto da figura? (Há definições mais abrangentes, mas essa servirá). É ela que você usa quando calcula a velocidade média (espaço sobre o tempo). E se souber como utilizá-la bem, poderá corrigir vários bugs irritantes facilmente.
Para começar, ligue os motores de um novo projeto (estou usando aqui o GM 8.0 PRO, você pode me chamar de atrasado se quiser) e crie um objeto.
Para isto, só utilizaremos dois eventos.
No evento Create, declare as seguintes variáveis:
- Código:
clique=0;
x=room_width*.5;
y=room_height*.5;
angle=360;
diferencial=.001;
xx=x;
yy=y;
dr=0;
Nem precisava de tudo isso, mas quero deixar as coisas mais claras possíveis. Basicamente, estamos dizendo que o objeto estará no centro da Room, o ângulo inicial será de 360 (ou 0, se você insiste). Das outras variáveis falaremos no próximo evento que será... agora.
DRAW
É aqui que a mágica acontece.
Em primeiro lugar, vamos estabelecer o tamanho do círculo. (Trigonometria, lembra?) Você pode evitar isso e voltar no Create, colocando o valor que quiser em r. Mas eu acho mais didático adicionar isso no Draw:
- Código:
if clique=0 {
r=point_distance(x,y,mouse_x,mouse_y);
};
if mouse_check_button_pressed(mb_left) {
if clique=0 clique=1;else clique=0;
};
Só mais um detalhe:
- Código:
if keyboard_check(vk_left) {
if angle<360 angle+=1;else angle=0;
}if keyboard_check(vk_right) {
if angle>0 angle-=1;else angle=360;
};
Agora vem a parte legal.
- Código:
ptx1=cos(degtorad(diferencial*.5+angle))*r+x;
pty1=-sin(degtorad(diferencial+angle))*r+y;
ptx2=cos(degtorad(-diferencial+angle))*r+x;
pty2=-sin(degtorad(-diferencial*.5+angle))*r+y;
Não desista ainda. Vamos com calma. Em Matemática, o cosseno refere-se ao eixo x, a ordenada horizontal, enquanto o seno colabora com o y. O GM não entende bem os ângulos como aprendemos no colégio. Ele usa radianos. 180º = π , em radianos, por exemplo. Por isso usamos a função "degtorad", ela converte graus em radianos.
Agora o que viria a ser esse "diferencial+angle" e o oposto? Bem, em Matemática, há um conceito bem útil chamado Limite. Basicamente, ele diz que um valor pode se aproximar muito de outro, sem realmente chegar nesse último, com valores infinitamente próximos daquele, mas nunca exatamente. O GM tem um probleminha com isso. Se você começar a dividir muito um número, ele não se aproxima de zero, depois da quarta casa decimal ele realmente chega a zero. Por isso, precisamos de um artifício: dois pontos, um muito próximo do outro. Próximo quanto? Volte no Create. 0,001 é próximo o bastante?
Assim: ptx1 e pty1 são as coordenadas do primeiro ponto e ptx2 junto à pty2 são as coordenadas do segundo ponto. Eles estão muito, muito próximos, mas não no mesmo lugar. Portanto, se você traçar uma linha que passe nesses dois pontos, parabéns, terá traçado a reta tangente.
Isto aqui só vai dar uma ambientada na Room para ela parecer um plano cartesiano:
- Código:
draw_set_color(c_black);
draw_line(room_width*.5,0,room_width*.5,room_height); //linha vertical
draw_line(0,room_height*.5,room_width,room_height*.5); //linha horizontal
draw_circle(x,y,r,1); //O nosso círculo!
draw_circle(x,y,r-1,1); //ainda ele
draw_text(16,16,"Raio: "+string(r)+"#Ângulo: "+string(degtorad(angle))+" ("+string(angle)+"º)#Seno: "+string(sin(degtorad(angle)))+
"#Cosseno: "+string(cos(degtorad(angle)))+"#Inclinação: "+string(tan(degtorad(angle)))); //Só para a gente ver como tudo está se comportando
Agora vamos desenhar os dois amiguinhos que estão muito perto, mas não exatamente no mesmo lugar:
- Código:
draw_set_color(c_white);
draw_circle(ptx1,pty1,r*.025,0);
draw_circle(ptx2,pty2,r*.025,0);
Agora, mais uns cálculos e eu juro que terminamos:
- Código:
dr=point_distance(x,y,(ptx1+ptx2)*.5,(pty1+pty2)*.5); //artificio para levar em conta a distância entre os pontos
xx=cos(degtorad(angle))*dr+x; //compare com ptx
yy=-sin(degtorad(angle))*dr+y; //compare com pty
dir1=degtorad(point_direction(xx,yy,ptx1,pty1)); //a primeira bolinha
dir2=degtorad(point_direction(xx,yy,ptx2,pty2)); //a segunda
Note que esses cálculos para xx e yy são muito parecidos com os para ptx e pty. Qual a diferença? Simples: eles não tem o diferencial, ao mesmo tempo que levam em conta a sua existência lá atrás. Representam o ponto médio, onde a nossa reta deve obrigatoriamente passar. Ela sai desse ponto médio rumo ao longe passando por dir1 que é o nosso primeiro ponto, e para o outro lado, passando por dir2, que é o segundo.
E agora, o grande final, onde você desenha a dita cuja, a reta tangente:
- Código:
draw_set_color(c_black);
draw_line_width(cos(dir1)*1000+xx,-sin(dir1)*1000+yy,cos(dir2)*1000+xx,-sin(dir2)*1000+yy,1);
Pessoal, essa foi uma demonstração de como utilizar certos artifícios no GM. Isso significa que você pode decompor fragmentos para usar no cotidiano. Afinal, a não ser que seja professor de matemática também, pode não precisar de um demonstrativo de seno, cosseno e tangente todos os dias.
Aqui você pode baixar a engine
(https://www.mediafire.com/?3b6vwoklpu6taue)
O resultado desse pequeno aplicativo que criamos é este:


Thiago_o_programador- Games Ranking :
Notas recebidas : D - C - D - C
Data de inscrição : 14/05/2009
Reputação : 7
Número de Mensagens : 713
Prêmios :
 x 0
x 0  x 0
x 0  x 0
x 0 x 0
x 0  x 0
x 0  x 1
x 1 x 0
x 0  x 0
x 0  x 0
x 0
 Tópicos semelhantes
Tópicos semelhantes» mais alguma coisa !
» Pessoal tem alguma conecção?
» Erro com alguma coisa
» By a whisker - Alguma ideia ?
» Existe alguma diferença de codigos nos GM 6 e 7?????
» Pessoal tem alguma conecção?
» Erro com alguma coisa
» By a whisker - Alguma ideia ?
» Existe alguma diferença de codigos nos GM 6 e 7?????
GMBR :: Ensine & Aprenda :: Tutoriais :: Game Maker
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
